 |
 |
Zionismens folkemord i Palæstina er i dag et barbari, der overgår nazismens terror i Europa under 2. Verdenskrig. Palæstinenserne er i dag verdens jøder, og zionisterne deres bødler |
Schrödingerligningen, formuleret af den østrigske kvantefysiker Erwin Schrödinger i 1925, beskriver tidsafhængigheden af kvantemekaniske systemer. Den har en betydning i kvantemekanikken svarende til Newtons 2. lov i den klassiske mekanik.
Indenfor kvantemekanikken kan sættet af alle mulige tilstande for et system beskrives ved et komplekst Hilbert rum, og systemets øjeblikkelige tilstand kan beskrives ved en enhedsvektor i dette rum. Denne tilstandsvektor er bestemmende for sandsynlighederne for alle resultaterne fra de forskellige målinger, systemet kan udsættes for. Eftersom systemets tilstand normalt ændres over tid, er tilstandsvektoren en funktion af tiden. Schrödinger ligningen giver en kvantitativ beskrivelse af ændringshastigheden af tilstandsvektoren.
I Diracs notation kalder vi den øjeblikkelige tilstandsvektor ved tiden t for |ψ(t)〉. Scrödinger ligningen siger da:
hvor i er det enhedsimaginære tal,
![]() er Plancks
konstant divideret med 2π, og den Hamiltonske H er den Hermitianske (selv-adjunkte)
lineære operator der påvirker tilstandsrummet. H beskriver systemets
samlede energi. Ligesom kraften der optræder i Newtons 2. lov, siger
Schrödingerligningen intet om dens eksakte form. Den må individuelt bestemmes ud
fra kvantesystemets fysiske egenskaber.
er Plancks
konstant divideret med 2π, og den Hamiltonske H er den Hermitianske (selv-adjunkte)
lineære operator der påvirker tilstandsrummet. H beskriver systemets
samlede energi. Ligesom kraften der optræder i Newtons 2. lov, siger
Schrödingerligningen intet om dens eksakte form. Den må individuelt bestemmes ud
fra kvantesystemets fysiske egenskaber.
For hvert H eksisterer der et antal kvantetilstande, der betegnes eigen-energitilstande. De opfylder eigenværdiligningen:
En sådan tilstand besidder en defineret samlet energi, hvis værdi E er eigenværdien af tilstandsvektoren med den Hamiltonske H. Denne eigenværdiligning betegnes også som den tidsuafhængige Schrödinger ligning. Hermitianske operatorer som den Hamiltonske har den egenskab, at deres eigenværdier altid er reelle tal. Dette var ventet, da energi er en fysisk observerbar størrelse. Vi kan nu indsætte den tidsuafhængige Schrödingerligning i den samlede Schrödingerligning:
Det er let at løse denne ligning. Vi finder at som tiden skrider frem ændres tilstandsvektorerne i eigen-energitilstandene kun med en kompleks fase:
Eigen-energitilstandene er hensigtsmæssige at arbejde med, fordi deres tidsafhængighed er så simpel. Det er grunden til, at den tidsuafhængige Schrödingerligning er så brugbar. Vi kan altid vælge et sæt af øjeblikkelige eigen-energitilstande, hvis tilstandsvektorer {|n〉}udgør en basis for tilstandsrummet. Enhver tilstandsvektor |ψ(t)〉 kan da beskrives som en lineær superpositionering af eigen-energitilstande:
![]()
(Den sidste ligning understreger kravet om, at |ψ(t)〉 som alle tilstandsvektorer skal være en enhedsvektor). Når vi anvender Schrödingerligningen på hver side af den første ligning, og når vi udnytter det faktum at energibasisvektorerne pr. definition er lineært uafhængige, får vi:
Hvis vi derfor kender opløsningen af |ψ(t)〉 i energibasis ved t = 0, så er dens værdi ved et senere tidspunkt givet ved:
Positionsbasis
Tilstandsrummet for mange (dog ikke alle) kvantesystemer kan rummes indenfor en positionsbasis. I denne situation kan Schrödingerligningen omformuleres til en partiel differentialligning for en bølgefunktion - et komplekst skalarfelt der er afhængig af sted og tid. Denne udgave af Schrödingerligningen kaldes også Schrödingers bølgefunktion.
Elementerne i denne positionsbasis kaldes positions eigentilstande. Vi indskrænker os nu til kun at betragte et enkelt partikel system, hvor hver positions eigentilstand kan skrives som |r〉, hvor r er en reel vektor. Dette kan fortolkes som en tilstand, hvor partiklen befinder sig i positionen r. I dette tilfælde er tilstandsrummet mængden af alle kvadrat-integrerbare komplekse funktioner.
Bølgefunktionen
Vi definerer bølgefunktionen som projektionen af tilstandsvektoren |ψ(t)〉 på positions basis:
Eftersom positions eigentilstandene udgør en basis for tilstandsrummet, er integralet over alle projektionsoperatorer lig identitetsoperatoren:
Dette udtryk kaldes opløsningen af identiteten. Vi kan derfor vise at:
hvor ψ(r, t)* betegner den komplekst konjugerede af ψ(r,t). Dette vigtige resultat viser os, at det absolutte kvadrat på bølgefunktionen integreret over hele rummet skal give 1.
Vi kan derfor fortolke det absolutte kvadrat på bølgefunktionen som sandsynlighedstætheden for, at partiklen befinder sig på et givet sted i rummet. Med andre ord er |ψ(r, t)|² d³r sandsynligheden ved tiden t for at finde partiklen i det endelige rum med volumen d³r omkring stedet r.
Vi har tidligere vist, at eigen-energitilstandene kun ændres med en kompleks fase, som tiden skrider frem. Det absolutte kvadrat af deres bølgefunktioner ændres derfor ikke over tid. Eigen-energitilstandene svarer derfor til en statisk sandsynlighedsfordeling.
Operatorer i positions basis
Operatorer A der virker på bølgefunktionen er defineret i positionsbasis ved:
Operatorene A på begge sider af ligningen er forskellige. Operatoren til højre virker på kets, mens den til venstre virker på skalarfelter. Det er almindeligt at bruge de samme symboler for både at beskrive operatorer der virker på kets, og de der virker på projektionen ind i basis. Normalt vil operatorens type være tydelig udfra sammenhængen, men dette er en mulig kilde til forvirring.
Schrödingers bølgeligning
Når vi anvender positionsbasis notationen kan Schrödingerligningen formuleres i positionsbasis som:
Denne udgave af Schrödingerligningen kaldes også Schrödingers bølgeligning. Det kan virke som om dette er en almindelig differentialligning, men i virkeligheden rummer den Hamiltonske operator typisk afledte ifht. positions variablen r. Dette efterlader os ofte med løsningen af en vanskelig ikke-lineær partiel differentialligning.
Ofte kan den Hamiltonske operator udtrykkes som summen af to operatorer, hvor den ene svarer til kinetisk energi, og den anden til potentiel energi. For en enkelt partikel med massen m, ingen elektrisk ladning og intet spin, kan udtrykket for den kinetiske energi skrives:
hvor p er impuls operatoren, defineret ved:
Den potentielle energi kan udtrykkes ved en reel skalarfunktion V = V(r), der beskriver den potentielle energi for partiklen i positionen r. Når vi lægger disse sammen får vi:
hvor ![]() 2
er Laplace. Dette er en hyppigt optrædende form af Schrödingers bølgeligning, om
end ikke den mest generelle.
2
er Laplace. Dette er en hyppigt optrædende form af Schrödingers bølgeligning, om
end ikke den mest generelle.
Løsninger for Schrödingerligningen
Analytiske løsninger af den tidsuafhængige Schrödingerligning kan formuleres for en række relativt simple systemer. Disse løsninger giver et vist indblik i kvantefænomenernes natur, og giver nogle gange en vis tilnærmelse til mere komplekse systemers opførsel. Indenfor statistisk mekanik kan molekylære vibrationer ofte tilnærmes ved en beskrivelse som harmoniske oscillatorer.
| Links til andre opslag i leksikonet | ||
Klassisk mekanik, Kvantemekanik, Newton, Isaac, Schrödinger, Erwin, Statistisk mekanik | ||

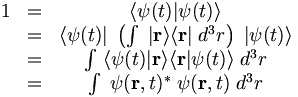
![\left[ - \frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}) \right] \psi(\mathbf{r}, t) =
i \hbar \frac{\partial \psi}{\partial t} (\mathbf{r}, t)](images/schrod_16.png)